第1章 群の概念
[定義]群
$$ G=\{ a, b, c, \cdots\} $$
有限または無限の集合$$G$$が,群groupと呼ばれるのは,次の公理を満たす場合である:
1° 2項演算の存在: $$ ^{ \forall }a, ^{ \forall }b \in G \to a \circ b \in G $$
2° 結合法則の成立: $$a \circ (b \circ c)=(a \circ b) \circ c$$
3° 単位元の存在: ある元 $$e \in G$$(ただ一つ)が存在し,
$$a \circ e=e \circ a=a$$が,すべての $$a \in G$$に対して成り立つ.
4° 逆元の存在: 各 $$a \in G$$に対して,
$$x \circ a=a \circ x=e$$となる $$x \in G$$が,いつも(ただ一つ)存在する.
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
[補足]
集合の元間に,演算$$ \circ $$(2項演算)が定義されて,その演算について,何らかの"構造"を持つ集合を,代数系($$ \circ $$系)という.群は,1種類の2項演算$${\circ}$$に関する代数系の例である.
・演算$$ \circ $$について結合的(1°,2°のみ成り立つ)である代数系は半群という.
・演算が定義できる2元と,できない2元を含む(1°に制限のある)複雑な代数系として,色々な亜群groupoidが定義される.
$$e_l \circ a=a$$となる$${e_l}$$を左単位元,$$a \circ e_r=a$$となる$${e_r}$$を右単位元という.群の公理3°は,群の右単位元と左単位元は同一であることを主張している.
$${e_l =a\circ x_r}$$となる$$x_r$$を$$a$$の右逆元,$${e_r=x_l \circ a}$$となる$${x_l}$$を$$a$$の左逆元という.群の公理4°は,右逆元と左逆元とが同一であることを主張している.
しかし,本当は,左単位元と右逆元の存在(あるいは,右単位元と左逆元の存在)だけ公理に入れればよい.
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
[演習]
■群の公理3°,4°で,”ただ一つ”というのは公理に含めなくてもよい(導くことができる).
●単位元が2つあったとし,それらを左単位元$${e_l}$$,右単位元$${e_r}$$とする.
$$e_r=e_l \circ e_r=e_l$$
ゆえに,右単位元と左単位元は同一であり,単位元を$${e}$$と記す.
●任意の元$${a}$$の逆元が2つ(左逆元$${x}$$,右逆元$${y}$$)あったとする.
$${e\circ y=x\circ a\circ y=x\circ e}$$ よって$${x=y}$$
従って,$${^{\forall}a}$$の右単位元と左単位元は同一になり,$${a^{-1 } }$$と記す.
■以下の等式を証明せよ.
■ $$(a^{-1})^{-1}=a$$
(証明) $$a \circ a^{-1}=a^{-1} \circ a=e$$
$$(a^{-1}) \circ (a^{-1})^{-1}=(a^{-1})^{-1} \circ (a^{-1})=e$$
$$(a^{-1})$$の逆元は一意であるから,$$(a^{-1})^{-1}=a$$
■ $$\left( a \circ b \right) ^{-1}=b^{-1} \circ a^{-1}$$
(証明) $$(a \circ b)^{-1} \circ (a \circ b)=e$$
$$(b^{-1} \circ a^{-1}) \circ (a \circ b)=e$$
ーーーーーーーーーーーーーーーーーーーーーーーーーー
群の例
例1. 整数$$Z=\left\{ 0, \pm 1, \pm 2, \cdots \right\} $$: 加法群をなす.
例2. 実数$$R$$: 加法で群
例3. $$R-{0}$$: 乗法で群
ーーーーーーーーーーーーーーーーーーーーーーーーー
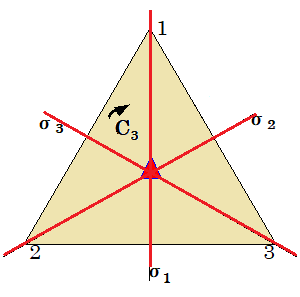
例4. 正3角形の3次の対称群(置換群)
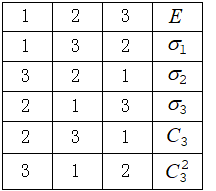
対称操作の表
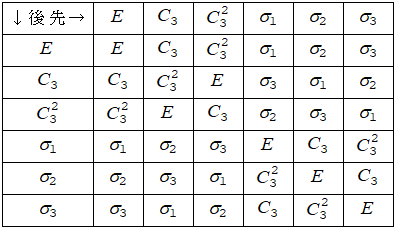
■乗積表
鏡映面$$\sigma _{1}, \sigma _{2}, \sigma _{3}$$は,図形のそれぞれの頂点に固定されて変換されるとして,群の乗積表を作りなさい.
乗積表
乗積表からわかること:
・群を作る$$ \longrightarrow $$ 3次の対称群(有限群,位数は6)
・可換群(Abel群)ではない.
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
例5.$$n$$次正則行列の集合
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
例6. $$n$$次直交行列 $$O(n)$$
$$A \in O(n)$$のとき,$$\left| \begin{array}{@{\,} c @{\, } }
A
\end{array} \right| $$を求めよ.$$\left| \begin{array}{@{\,} c @{\, } }
A
\end{array} \right| =\textrm{det}A$$は行列式の記号
$$\left| \begin{array}{@{\,} c @{\, } }
^{t}AA
\end{array} \right| =\left| \begin{array}{@{\,} c @{\, } }
E
\end{array} \right| $$ $$\Longrightarrow$$ $$\left| \begin{array}{@{\,} c @{\, } }
A
\end{array} \right| ^{2}=1$$ $$\Longrightarrow$$ $$|A|= \pm 1$$
これを回転群と呼ぶ.
■$$A \in SO(2)$$のとき,適当に$$\theta $$をとって,
$$A=\left( \begin{array}{@{\,} cc @{\, } }
\textrm{cos}\theta & -\textrm{sin}\theta \\[0mm]
\textrm{sin}\theta & \textrm{cos}\theta
\end{array} \right) $$ と書くことができる.
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
[定義] 元の位数$$r$$
元$$a$$の位数$$r$$とは,$$a^{r}=e$$となる最小の自然数である.
このような$$r$$がないときは,元$$a$$は自由元である.
有限群の位数とは,元の数である.
-----------------------------
集合の2元間に或る2項演算$$ \circ $$が定義され,その演算$$ \circ $$に関して,或る「構造」を持つ集合を代数系という.
演算$$ \circ $$は結合法則 $$\left( x \circ y \right) \circ z=x \circ \left( y \circ z \right) $$が成立つ.
演算$$ \circ $$について,結合法則だけが存在する代数系を「半群」という.
-----------------------ーーーーーー
[定義]群の軌道
群$$\mit\Gamma $$を,集合$$X$$上に作用する「変換群」とする.
群$$\mit\Gamma $$による$$a \in X$$の軌道とは,$$\mit\Gamma (a)=\left\{ \sigma (a)|\sigma \in \mit\Gamma \right\} $$.
$$X \ni a, b$$に対して,$$b$$が$$a$$の軌道に含まれるという関係は,$$X$$における同値関係になる.
軌道は同値類で,集合$$X$$を軌道で類別できる.
$$X$$の中に軌道がただ一つしかない場合:
つまり,$$^{ \forall }x, ^{ \forall }y \in X$$に対して,$$^{ \exists }\sigma \in \mit\Gamma $$があり,$$\sigma (x)=y$$のとき,$$\mit\Gamma $$は推移的という.
[演習]
軌道に属するという関係は,同値関係であることを確認せよ.
$$a$$の軌道に$$b$$が含まれるとする:$$ b \in \left\{ \sigma (a)|\sigma \in \mit\Gamma \right\} $$であるから,$$b=\sigma _{i}(a)$$となる$$^{ \exists }\sigma _{i} \in \mit\Gamma $$がある.$$\mit\Gamma $$は群であるから,$$\sigma _{i}^{-1} \in \mit\Gamma $$があり,$$\sigma _{i}^{-1}(b)=a$$となり,$$b$$の軌道に$$a$$が含まれる.ゆえに,$$ {\mit\Gamma}(a)={\mit\Gamma} (b) $$.
これは,対称律を保証する.反射律,推移率も同様に成立する.